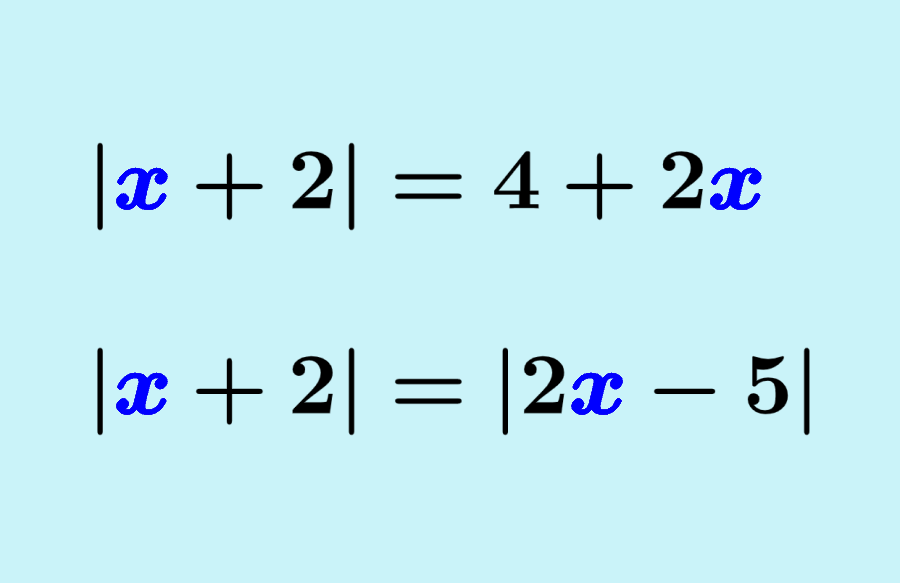Despejes de Ecuaciones Lineales

COMO DESPEJAR LAS ECUACIONES LINEALES

Las ecuaciones son una herramienta fundamental en el mundo de las matemáticas. A través de ellas, podemos resolver problemas y encontrar soluciones. Sin embargo, en muchas ocasiones, estas ecuaciones pueden resultar confusas y complicadas de resolver debido a la presencia de variables. Por eso, en este artículo te enseñaremos cómo despejar variables en ecuaciones de manera sencilla y práctica.

Lo primero que debes saber es que despejar una variable en una ecuación consiste en aislarla para que quede sola en un lado de la igualdad. Para hacerlo, es necesario aplicar una serie de operaciones matemáticas que permitan simplificar la ecuación y llegar al resultado deseado.

Para entender mejor este proceso, veamos un ejemplo práctico:

Ejemplo:

Despejar la variable «x» en la siguiente ecuación: 2x + 3 = 11

1. Lo primero que debemos hacer es restar 3 a ambos lados de la ecuación:

2x + 3 – 3 = 11 – 3

2. Simplificamos:

2x = 8

3. Para despejar la variable «x», dividimos ambos lados de la ecuación por el coeficiente que acompaña a «x», en este caso 2:

2x/2 = 8/2

x = 4

Con estos pasos hemos logrado despejar la variable «x» y encontrar su valor en la ecuación.

Es importante recordar que este proceso se puede aplicar a cualquier tipo de ecuación, ya sea lineal, cuadrática, etc. Lo fundamental es tener claro el objetivo de despejar la variable y aplicar las operaciones matemáticas de manera ordenada y sistemática.

A través de la práctica y el conocimiento de las diferentes operaciones matemáticas, podemos resolver ecuaciones de manera sencilla y eficiente. ¡Anímate a practicar y verás que se trata de una tarea más fácil de lo que parece!

Mas Información Consulte Aquí

Ecuaciones Fraccionarias

ECUACIONES FRACCIONARIAS 

 No son pocas las aplicaciones conducen  a ecuaciones en las que la variable aparece en el denominador, es decir en las que aparecen fracciones algebraicas y se les denomina ecuaciones fraccionarias, por ejemplo: 

En general las ecuaciones fraccionarias se resuelven transformándolas en ecuaciones mas sencillas o enteras. Por ejemplo, para resolver la ecuación con fracciones 

se busca el mcm entre los denominadores que aparecen en la ecuación, en este caso 2, 6 y 3. El mcm es 6 y aplicando las propiedades para obtener una ecuación equivalente multiplicado en ambos miembro de la  ecuación por el mcm. Así:

Lo cual nos permite obtener el valor de x:

En general, para resolver las ecuaciones fraccionarias se transforman en ecuaciones equivalentes enteras eliminando los denominadores y para ello se multiplica por el mcm de los denominadores, cuidando de excluir del dominio de la ecuación valores que anulen los denominadores donde aparezca la variable.

Es decir, para resolver una ecuación fraccionaria, se procede de la siguiente manera:

1. Se precisa el dominio de la ecuación, excluyendo los valores que anulen algún denominador.
2. Se halla el mcm de los denominadores.
3. Se multiplican ambos miembros de la ecuaciones  por el mcm de los denominadores.
4. Se resuelve la ecuación entera equivalente obtenida. 
5. Se comprueba la raíz o solución obtenida. 

Mas Información Consulte Aquí

Ecuaciones Fraccionarias

SOLUCION DE UNA ECUACION FRACCIONARIA 

Veamos al importancia de precisar el dominio de la ecuación en el caso de las ecuaciones fraccionarias, así como, una vez más, de la comprobación del resultado obtenido. Para ello, vamos a partir de la ecuación

1.   El dominio de la ecuación es R \ {-1, 1}

2.   El mcm de los denominadores es x2 - 1 = (x + 1) (x - 1).

3.   Si multiplicamos ambos miembros de la ecuación por el mcm y se realizan las operaciones indicadas          se obtiene       

                                                                           x + 1 + x - 1 = 2

4.   Resolviendo al ecuación resulta: 2x = 2

                                                           x = 1

5.   Si sustituimos por x = 1 en la ecuación original, para comprobar, se anulan dos denominadores y la            división por 0 no está definida, luego, aunque x = 1 es raíz de la ecuación que se obtuvo al                          transformar  la ecuación dada, no es raíz o solución de la ecuación original.

Ello se debe a que se ha multiplicado en ambos miembros por un factor que, aunque es el mcm, anula un denominador de la ecuación original, ya que el valor x = 1 no está en el dominio de la ecuación. En estos casos se dice que se ha introducido una raíz extraña, que es solución de la ecuación transformada pero no de la original, por tanto, ambas ecuaciones no son equivalentes.

La ecuación dada no tiene solución.

Mas Información Consulte Aquí

Solución de ecuaciones con doble valor absoluto

 Solución de ecuaciones con doble valor absoluto 

Vamos a resolver la ecuación 2|x| +|x - 1|= 2.

Analicemos primeramente, por separado, los dos valores absolutos que aparecen en la ecuación.

Representemos lo obtenido en un esquema:

Por tanto, quedan definidos tres intervalos en los que hay que analizar los posibles valores de x: 

(-∞, 0), [0, 1) y [1, +∞).

Si -∞ < x < 0, entonces |x| = -x y |x - 1| = -(x- 1) luego

                    2(-x) - (x - 1) =2 ⇔ -2x - x + 1 = 2 ⇔ -3x = 1 ⇔ x = -1/3.

Si 0 ≤ x < 1, entonces |x| = x y |x - 1| = -(x - 1) luego

                2x - (x - 1) = 2 ⇔ 2x - x + 1 = 2 ⇔ x = 1, pero este valor no está en ese intervalo.

Si 1 ≤ x < +∞, |x| = x y |x - 1| = x - 1, luego

                2x + (x - 1) =2 ⇔ 2x + x - 1 = 2 ⇔ 3x = 3 ⇔ × = 1

Comprobación:

Para x = -1/3, el MI es: 2|-1/3| + |-1/3 - 1| = 2/3 + 4/3 = 2, lo que coincide con el MD

Para x = 1, el MI es: 2|1| + |1 - 1| = 2 + 0 = 2, que igualmente coincide con el MD.

Por tanto -1/3 y 1 son las raíces o soluciones de la ecuación.

Mas Información Consulte Aquí

Ecuaciones Lineales con valor absoluto 

Si a es un número real, |a| = a, si a ≥ 0 y |a| = -a, si a < 0.

Entonces, una igualdad como |x| = 4, en la que aparece el valor absoluto o módulo de la variable x, es básicamente una ecuación en la que para determinar el valor de x cómo incógnita aplicamos la definición de valor absoluto; luego, utilizando el símbolo ⇔ (equivale a) se tiene

De esta forma, si tenemos la ecuación |x - 1| = 4, por la definición de valor absoluto 

Si comprobamos, |5 - 1| = 4 y |-3 - 1| = 4, luego las raíces de esta ecuación son -3 y 5.

Ecuaciones como la anterior, que contienen la variable dentro del signo de módulo o valor absoluto, se definen como ecuaciones con valor absoluto o modulares. En estas ecuaciones es posible determinar su solución tanto analíticamente como gráficamente.

Geométricamente |x| = 4 significa que la distancia entre x y el punto que representa al 0 es 4:

De igual forma |x - 1| = 4 significa que la distancia que hay entre x y 1 es 4; estos son los puntos que representan a -3 y 5, como se ve en el gráfico, y que coincide con lo obtenido analíticamente.

De manera general, si a y b son dos números reales cualesquiera, se tiene que la distancia entre a y b está dada por:

                                                       d(a, b) = |b - a| = |a - b|

Mas Información Consulte Aquí

ECUACIONES LITERALES LINEALES

¿QUE SON  LAS ECUACIONES LITERALES LINEALES?

Una ecuación literal es aquella en la que una o más de las cantidades conocidas se representan mediante el uso de letras. Por lo general, dichas cantidades conocidas se representan con las primeras letras del alfabeto a, b, c... y las incógnitas con las letras finales x, y, z .

Ejemplo:

a + bx = dy

En este ejemplo las letras a, b, d, son cantidades conocidas, mientras que x e y, representan las incógnitas de la ecuación.

Otro ejemplo de este tipo de ecuaciones, lo podemos encontrar en fórmulas de perímetros, áreas, volúmenes, etc. donde se haga uso de literales.

Para resolver estas ecuaciones se aplican las mismas reglas que se utilizan en la resolución de ecuaciones ordinarias:

Primero, se efectúan las operaciones indicadas, si las hay.

Luego, se trasladan los términos, para agrupar en un miembro los términos que contengan la incógnita y en el otro miembro, los términos que no contienen la incógnita y por lo tanto son conocidos (aunque estén expresados con letras).

En un tercer paso, lo prudente es reducir los términos semejantes en los dos miembros, para que sea más fácil el manejo de la incógnita.

Se despeja la incógnita. Para poder despejar la incógnita, es útil recordar que en una igualdad podemos hacer operaciones iguales a los dos miembros, sin alterar la igualdad.

x + 3 = 10

Para despejar la incógnita "x", debemos restar 3 a cada miembro de la igualdad:

x + 3 – 3 = 10 – 3

Para que de esta forma, quede:

x = 7

Esta regla se aplica a cualquiera de las operaciones que afecten a la incógnita:

Ejemplos:

a) 5x = 8x –15

Lo primero que debemos hacer es colocar en un miembro todos los términos que contengan la incógnita, es decir, restemos 8x a los dos miembros, para obtener:

5x – 8x = 8x – 8x –15

Al reducir términos semejantes, tendremos:

–3x = –15

Si multiplicamos los dos miembros por (–1), obtendremos:

(–3x)(–1) = (–15)(–1)

3x = 15

Si dividimos los dos miembros entre 3, nos resulta que:

x = 5 que es el único valor en que se cumple la igualdad

Mas Información Consulte Aquí

Aplicaciones de las ecuaciones lineales

 APLICACIONES DE LAS ECUACIONES LINEALES

Las ecuaciones lineales permiten interpretar y resolver mediante la modelación matemática diversas situaciones en la propia matemática y otras ciencias, así como en esferas de la vida cotidiana. La solución de estos problemas comienza por interpretar correctamente la situación que se presenta, llevar al lenguaje algebraico la problemática planteada y resolver ecuaciones. A modo de motivación, veamos el siguiente problema que pudiera parecer confuso, pero no lo es.

Un holgazán duerme normalmente cada día todas las horas del día menos las que duerme. ¿Cuántas horas permanece despierto diariamente? ¿Ninguna?

Veamos cómo llevar este problema al lenguaje algebraico y resolverlo.

El día tiene: 24 horas.

• ¿Cuántas horas permanece despierto? No sabemos, es una incógnita: x

• ¿Cuántas horas duerme? Serán: 24 - x

Duerme cada día todas las horas menos las que duerme, es decir ¿las qué debiera estar despierto?

por tanto, x = 24 - x, estamos en presencia de una ecuación lineal con una incógnita.

Entonces, aplicando las reglas para resolver ecuaciones:

x = 24-x

x + x = 24

2x = 24

x = 12.

Comprobación: El propio enunciado del problema permite razonar que, si duerme todas las horas del día menos las que duerme, sólo duerme esas horas. Si obtuvimos como horas en que está despierto

que x = 12, entonces duerme 24 - 12 = 12. Eso cumple el enunciado del problema, es decir duerme todas

las horas (12) menos las que duerme, que es la diferencia con 24, que es 12. Por tanto, el holgazán está despierto 12 horas al día.

En esta sección vamos a ejemplificar problemas que se resuelven utilizando las ecuaciones lineales con una incógnita. Ello requiere de mucha práctica y de lograr expresar correctamente en lenguaje algebraico las condiciones del problema planteado.

Sin que constituya un esquema, es recomendable dar los siguientes pasos que son de utilidad en la solución de problemas:

1. Ante todo, lee cuidadosamente el enunciado del problema, hasta estar seguro que comprendes

perfectamente la situación planteada.

2. Determina cuáles son los datos conocidos y los que no conoces, que serán las incógnitas.

3. Si hay una sola incógnita identifícala con una letra, si hay más de una hay que expresar los demás valores desconocidos en términos de la incógnita que ya se ha identificado con una letra.

4. Determina en el enunciado del problema las relaciones que te permitan formular una ecuación.

5. Resuelve la ecuación obtenida.

6. Comprueba la solución obtenida directamente en el enunciado del problema, no en la ecuación.

7. Da la respuesta en función de lo que se pide en el enunciado del problema.

Ejemplo

El triplo de un número es igual al número aumentado en 8. Hallar el número.

1. El problema se refiere a relaciones que cumple un número que no se conoce.

2. Estas relaciones se refieren a 3 veces el número y al número más 8.

3. Denotamos el número desconocido por x.

4. De acuerdo con el enunciado, 3 veces el número es igual al número más 8, es decir

3x = x + 8.

5. Resolvemos la ecuación trasponiendo x y aplicando transformaciones equivalentes.

3x = x+8

2x = 8

x = 8/2

x= 4

6. Comprobando: Tres veces el número encontrado 4 es 12 que es lo mismo que el número 4

aumentado en 8.

7. Respuesta: El número buscado es 4.

Mas Información Consulte Aquí